Combinatoric Logic Game of Marbles

Combinatoric Logic Game of Marbles
Armahedi Mahzar (c) 2015

In my previous blog it has been shown that the combination and disposal of parallel colorful sticks with two orientations can prove any valid syllogism tabulated by Leibniz by the lineal combinatoric of Ploucquet. The combinatoric verification process can also be simulated by the game of arranging and disposing colored marbles and pieces of paper.

In the following it will be shown that we can simulate logical proof with the game arranging and disposing  the colorful marbles and pieces of paper. The secret is the fact that we can replace the changing the line length to represent the opposite concept with the changing of the marble’s ground.

Fundamental Categorical Proposition of Aristotle

If the subject a is represented by a red marble   and predicate b represented by green marble  , then NOT a is represented by red marble placed upon small white paper  .
Furthermore, the fundamental categorical statement of Aristotle is represented by pairs of marbles as it is shown in the following table

The premises and conclusion of a syllogism form is one of four such statements.

Proof of the Validity of Syllogism

The game playing that simulate the proving of the validity of a syllogism includes the following steps

1. juxtaposing the marble pairs which represent both premises of a syllogism
2. disposing the pair of same colored marble with different ground
3. putting the marble which represent the subject of the second premise as the marble that represent the subject of the syllogism conclusion.

With a game like this, we can do the proving of valid syllogisms with ease, because the end result of the game is a representation of the syllogism conclusion. The table below is the Leibniz table of the premises of valid syllogisms.

 

End notes

1. Apparently, the game is very simple using colored marbles  can be taught to kindergartners. The game can also be seen as a simulation of Sommersian arithmologic.
2. Unfortunately, this game can only be played with the help of additional pieces of paper,  however, with a set of colored cards without  the help of other pieces of paper, we can simulate the proving of the syllogism validity with a simpler game as I have found it. Hopefully, that will be presented in my next blog.

Combinatoric Logic Game of Sticks

Combinatoric Logic Game of Sticks
Armahedi Mahzar (c) 2015

In my previous blog it has been shown that the combination and disposal of parallel colorful lines with two size can prove any valid syllogism tabulated by Leibniz by the lineal combinatoric of Ploucquet. The combinatoric verification process can be simulated by the game of arranging and disposing colored lines of two lengths.

In the following it will be shown that we can also make the game loading and stacking the colorful sticks with only one size. The secret is the fact that we can replace the changing the line length to represent the opposite concept with the changing of the stick orientation.

Fundamental Categorical Proposition of Aristotle

If the subject is represented by a red upright stick and predicate b represented by green upright stick, then the fundamental categorical statement of Aristotle is represented by pairs of rods as it is shown in the following table

The premises or the conclusion of a syllogism is one of four such statements.

Proof of the Validity of Syllogism

The game playing that simulate the proving of the validity of a syllogism includes the following steps

1.   juxtaposing the stick pairs which represent both premises of a syllogism
2.   disposing the pair of same colored sticks with different orientation
3.   putting the stick which represent the subject of the second premise as the stick that represent the subject of the syllogism conclusion.

With a game like this, we can do the proving of valid syllogisms with ease, because the end result of the game is a representation of the syllogism conclusion that we can be compared to Leibniz's conclusions in the table below:

End notes

1. Apparently, the game is very simple using colored sticks that it can be taught to kindergartners. The game can also be seen as a Sommersian arithmologic game.

2. Unfortunately, this game can only be played with elongated objects such as a stick, but not to objects of arbitrary shapes.

3. God willing, with the help of pieces of paper, the proving of the syllogism validity can also be simulated by a game  on arbritrary things as I find it. Hopefully, that will be presented in my next blog.

Lineal Combinatoric of Ploucquet

Lineal Combinatoric of Ploucquet
Armahedi Mahzar (c) 2015

 

 In the last blog it has been shown that the literal combinatoric of Ploucquet can be used as a tool to seek the conclusion of a valid syllogism, simpler than the Boolean, Peircean or Sommersian arithmologic. The secret is that we replace the arithmetic operations with combinatoric operations, while elimination of the oppositely signed variables is replaced by the deletion of capital lower-case letters. Literal combinatoric method of  Ploucquet is indeed simple, but if writing letters are replaced with drawings colored lines, then the syllogism becomes more visual and the method can be easily taught in a pre-schooler who can not read letters. 

Therefore, in a method visualizing the literal combinatoric of  Ploucquet we can:

• Replacing the lowercase letters with short lines
• Replacing the capital letters with long lines
• Changing the names of the letters with the colors of the lines

Thus, in this method of lineal combinatoric

• variables are represented by short lines
• negation of variables are represented  by long lines
• conjunction is expressed by the juxtaposition 

Fundamental Categorical Propositions of Aristotle

If a = and b = , then the fundamental categorical propositions of Aristotle is described as follows 

The premises and conclusion of a syllogism are one of these four statements.

Proving the vadity of syllogism

With line images in this notation we can prove the validity of syllogism. For example, proving the validity of the syllogism Barbara in the lineal combinatoric methods color line is as follows
Abc AND Aab =

= Aac

 

Proving the validity of the other syllogism can be seen in the Leibniz table below

Leibniz-Ploucquet table of valid Syllogism

Concluding Remarks

1. Actually, the colored lines in the above method is a simplification of the following line method of Ploucquet 
 

where universality replaced with negativity and the two-dimensional arrangement (from the bottom to the top / from left to right) is replaced with a one-dimensional linear array (from left to right) of upright lines.

2. Game of colored lines with different length as a simulation logical deduction can be simplified by playing a one-sized colored sticks with different orientations. This game of logic is what we will be discussed in the next blog.

Literal Combinatoric of Plouquet

Literal Combinatoric of Plouquet

 Armahedi Mahzar (c) 2015

 

Gottfried Ploucquet
(1716-1790)

In previous blog, I pointed out that there are three kinds of arithmologic (Boole, Peirce and Sommers) but all three are structurally similar to each other. Essentially any arthmological statement is expressed as string of letters and symbols of mathematical operations. \
In this blog I will present a simpler literal combinatoric method which is inspired by Ploucquet nethod in the 18th century, before Boole introduced the algebraic symbolism for logic in the 19th century. The method is presented as combinatoric literalization of Sommersian arithmologic.

Arithmologic

The following are the arithmological symbols
+===============================================+
|                 Concept TRUE     FALSE     NOT       OR       AND      |
+——————————————————————————--+
| Boole        letter         1                 0           1-           +          -1+        |
| Peirce       letter         0                 1           1/           +                        |
| Sommers  letter                                        –             +            +         |
+——————————————————————————--+
Similarity of of the formulas can be shown by the following table of syllogism
+===========================================+
| Syllogism IF p AND q THEN r                                              |
|                              = NOT (p AND q) OR r                             |
+————————————————————————–+
| Boole                      1-(p-1+ q)+r = 1-p+1-q+r                        |
| Peirce                      1/(pq/r)    = 1/p 1/q r                               |
| Sommers                  -((p+q)-r)  = -p -q+r                              |
+——————————————————————--—–+
Proving its validity has also a similar procedure, namely:
the annihilation of pairs of oppositely signed variables.
Seeing the structural and procedural similarities, we can expect that there is a simpler symbolic formulation. The following is one of its simplification. For simplicity, I will use the Sommersian arithmologic as a reference, because it is the simplest.

Combinatoric Simplification of Arithmologic

To simplify the Sommersian arithmologic, we can use the following literalization conventions:
– Write the + sign with no spaces or symbols at all
– Write -x as the uppercase X.

Categorical statement of Aristotle

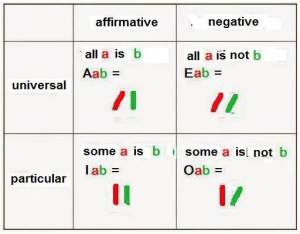
By shortening convention, we can write Aristotle fundamental categorical statement as follows:
(1) Universal affirmative
Aab = ‘all A is B’
can be written as Ab
(2) Universal negative
Eab = ‘no a is b’
can be written as AB
(3) Particular Affirmative
Iab = ‘some a are b’
can be written as ab
(4) Particular Negative denial
OAB = ‘some a are not b’
can be written as aB.

Validity proof of syllogism

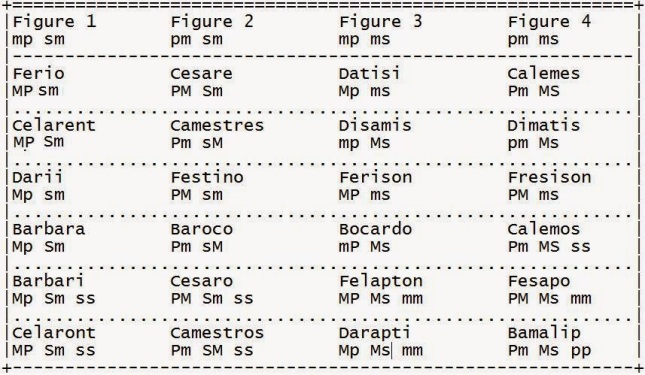
In this notation the verification algorithm of the validity of 24 syllogism Leibnitz in the following table

,
becomes very simple:
Step 1: write a joint symbol for premises
Step 2: delete the upper/lower case pair of letters.
The algorithm is becoming more concise and easier than the arithmologic.
Even elementary school children can do
We will make the proofs of all valid syllogism in column 1 in the Leibniz table now.
Barbara proof is
Abc AND Aab = Ab Bc = Ac = Aac
Celarent proof is as follows
Ebc AND Aab = Ab BC = AC = Eac
and Darii proof is like this
Abc AND Iab = ab Bc = ac = Iac
Similarly, the proof of Ferio is
EBC AND Iab = ab BC = aC = ​​Oac
To prove the existential syllogism proof is also simple.
Barbari proof is as follows
Eaa AND Aab AND Abc = aa Ab Bc = ac = Iac
and the Celaront proof islike this
Eaa AND Aab AND EBbc = aa Ab BC = aC = ​​Oac.
Syllogisms in the other columns also can be proven in the same way. Just use the Leibniz-Ploucquet table below


Well, this is very easy expression. The formula, with no signs of any math, is a mere string of small and capital letters. While the algorithm is not arithmetical but purely combinatorical.
Thus the method becomes very easy as well: merge premises and delete letter pairs.

End notes

Because this method is similar to the letter method Plouquet, I shall call it as Ploucquet logical method of literal combinatoric. The notation for the negative is similar to the notation of Ploucquet for universality.

However, Ploucquet also have a more visual method, namely the method of lineal combinatorics that, I think, is easier than the method of literal combinatoric. Hopefully, I will show a simplification of the literal Ploucquet method with the pictorial.