Combinatoric Logic Game of Sticks

Combinatoric Logic Game of Sticks
Armahedi Mahzar (c) 2015

In my previous blog it has been shown that the combination and disposal of parallel colorful lines with two size can prove any valid syllogism tabulated by Leibniz by the lineal combinatoric of Ploucquet. The combinatoric verification process can be simulated by the game of arranging and disposing colored lines of two lengths.

In the following it will be shown that we can also make the game loading and stacking the colorful sticks with only one size. The secret is the fact that we can replace the changing the line length to represent the opposite concept with the changing of the stick orientation.

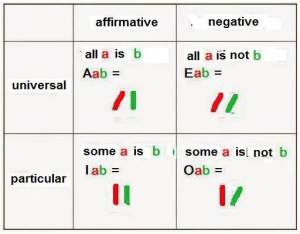
Fundamental Categorical Proposition of Aristotle

If the subject is represented by a red upright stick and predicate b represented by green upright stick, then the fundamental categorical statement of Aristotle is represented by pairs of rods as it is shown in the following table

The premises or the conclusion of a syllogism is one of four such statements.

Proof of the Validity of Syllogism

The game playing that simulate the proving of the validity of a syllogism includes the following steps

1.   juxtaposing the stick pairs which represent both premises of a syllogism
2.   disposing the pair of same colored sticks with different orientation
3.   putting the stick which represent the subject of the second premise as the stick that represent the subject of the syllogism conclusion.

With a game like this, we can do the proving of valid syllogisms with ease, because the end result of the game is a representation of the syllogism conclusion that we can be compared to Leibniz's conclusions in the table below:

End notes

1. Apparently, the game is very simple using colored sticks that it can be taught to kindergartners. The game can also be seen as a Sommersian arithmologic game.

2. Unfortunately, this game can only be played with elongated objects such as a stick, but not to objects of arbitrary shapes.

3. God willing, with the help of pieces of paper, the proving of the syllogism validity can also be simulated by a game  on arbritrary things as I find it. Hopefully, that will be presented in my next blog.