Boolean Syllogistic Game of Chips and Cards

Boolean Syllogistic Game of Chips and Cards
Armahedi Mahzar (c) 2016

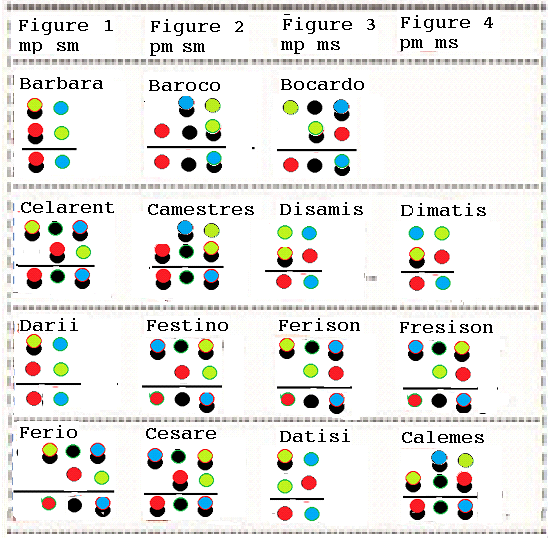
Lately, I had finally proved the validity of the 24 syllogisms as it is discovered by Leibniz using object algebra which is the total pictorialization of the Kauffman Box Algebra which is the equivalent formalization of the pictorial primary algebra of George Spencer Brown using the CROSS symbol.

I was so excited, I thought that I had found the simplest formalization of syllogistic after discovered the complexity of George Boole equation representing the solution of the the general syllogisms in his book the Laws of Thought.

The Elective Algebra

But later on I know that I was wrong, since later I discovered an article The Calculus of Logic by Boole in 1848 before he published his Laws of Thought in 1853.

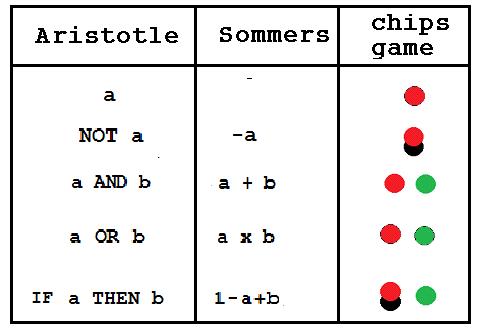
He called his logical calculus as the elective calculus. In this calculus he represented the four categorical propositions of Aristotle as simple linear equations.

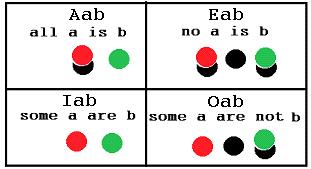
All x is y was written as x=ay, No x is y as x=a(1-y), some x is y as ax=by and some x is not y as ax=b(1-y). The conclusion of a syllogism is calculated by elimination the same variable in the equations represent the premises.

Using the new notation used by computer scientists All x is y was written as x=ay, No x is y as x=ay’, some x is y as ax=by and some x is not y as ax=by’

The Game of Chips and Cards

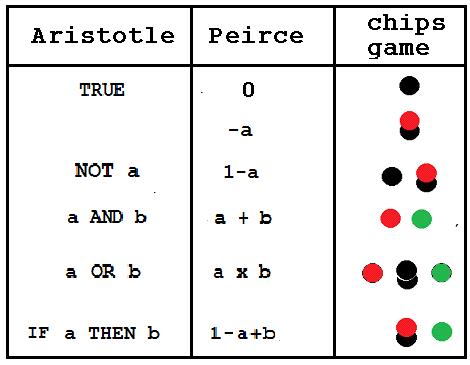
I was dumbfounded to find out the simplicity of the method. I used it for all first figure syllogisms. Inspired by my success to simulate Kauffman Box algebra with a game of things, I try to simulate the elective calculus proofs in a kind of game of thing.

All I need is a piece of paper and different colored chips to represent the variables and cards to represent the constant coefficients.

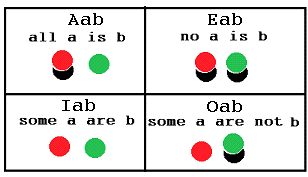
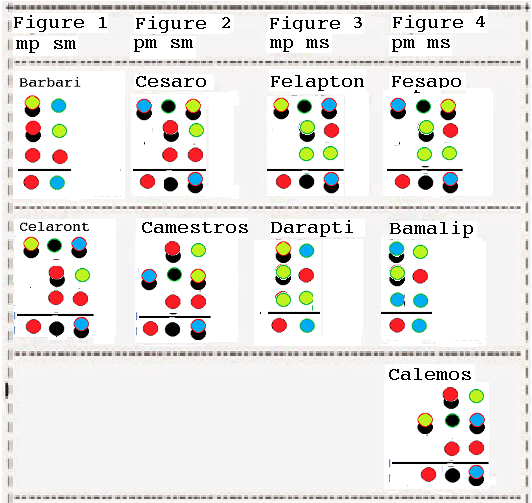
The game represents the categorical propositions of Aristotle as an arrangement of chips and cards inside and outside the paper according certain formation rules. The premises are represented by chip box arrangement.

The following table is the game representation of the categorical propositions of Aristotle which are represented by Boole as linear equations. The left side of the equation is represented by chip and card outside a piece of paper. The right side is represented by chip and card upon the paper.

Simulating the deductions

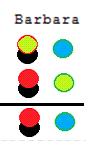
The premises are placed in the paper according the above rules then we get the conclusion by following transformation rules. The conclusion can be established by removing the pair of chips with same color positioned in and outside the paper and replacing the the pair of cards of different colors with a single card of another color. 

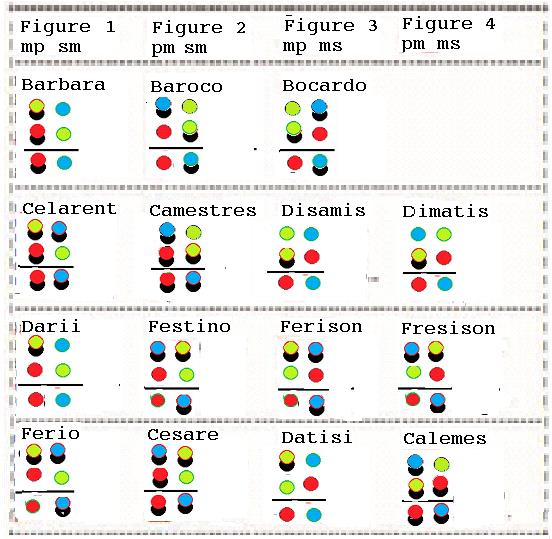
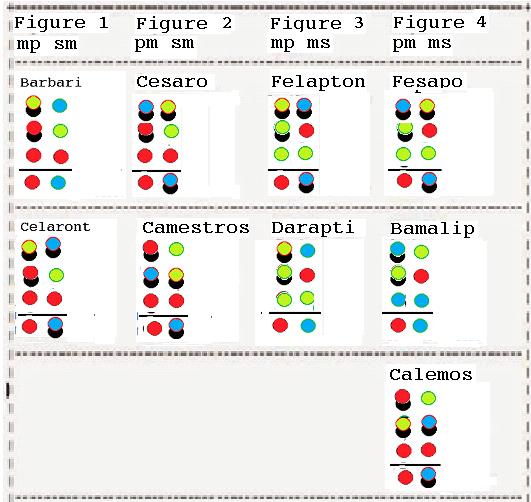
In the following picture it is shown the two steps transformation to deduce the conclusion of the syllogisms of the first figure

Barbari and Celaront can be gotten by adding a representation of some x is x or Ixx to the conclusion of Barbara and Celarent respectively and transforming the result by following the simple transformation rules above.

The syllogisms in the other column of the following Leibniz table



can be proved by showing that the conclusion of it can be gotten by following the same easy rules of transformation. How can it be done left as exercises for the readers.

Afternote

The syllogistic game as it is shown above is very simple so it can be taught to a kindergarten kid. However though it can conclude the conclusion of all valid syllogism. It also prove a conclusion from invalid syllogisms. So we need another game simulation for Boolean algebra. I hope I will explained the arithmetical method using Boole original notation in the next blog and simulate it in another kind of game of things.

Combinatoric Logic Game of Marbles and Cards

Combinatoric Logic Game of Marbles and Cards

Armahedi Mahzar (c) 2015

In my previous blog it has been shown that the arrangement and disposal of pairs of colorful cards with two orientation can prove any valid syllogism tabulated by Leibniz. The combinatoric verification process is simulated by the game of arranging and disposing colored cards  with two orientations.

In the following it will be shown that we can also make the game arranging and disposing anything with the help of a piece of paper. The secret is the fact that we can replace the changing the card orientation to represent the opposite concept in the last game with the changing of the thing position relative to the paper in the new game. In this blog we will use marbles and a piece of card as the pieces of the new logic game.

Fundamental Categorical Proposition of Aristotle

If concept a is representing by a marble   , the its opposite NOT a is represented by the the same marble inside the border of a card 

 .

If the subject is represented by a red marble and predicate b represented by green marble , then the fundamental categorical statement of Aristotle is represented by pairs of marbles will be shown in the following table

The premises and conclusion of a syllogism is one of four such statements.

Proof of the Validity of Syllogism

The game playing that simulate the proving of the validity of a syllogism includes the following steps
 

1. juxtaposing the marble pairs which represent both premises of a syllogism
2. disposing the pair of same colored marbles with different positions
3. putting the marble which represent the subject of the second premise as the marble that represent the subject of the syllogism conclusion.

With a game like this, we can do the proving of valid syllogisms with ease, because the end result of the game is a representation of the syllogism by disposing pair(s) of 
colored marbles in opposite positions in the  Leibniz’s  table below:

End notes

1.  The colored marbles can be replaced with anything that has duplicates and the card can be replaced with any sheet of paper.

2. The rules of forming the premises can be reversed. Thing outside the border of the paper is representing a universal or negative variable and the inside one is representing particular and positive variable.

Combinatoric Logic Game of Cards

Combinatoric Logic Game of Cards

Armahedi Mahzar (c) 2015

In my previous blog it has been shown that the combination and disposal of pairs of colorful marbles with two condition can prove any valid syllogism tabulated by Leibniz. The combinatoric verification process can be simulated by the game of arranging and disposing colored marbles with pieces of paper.

In the following it will be shown that we can also make the game arranging and disposing colorful cards with only two orientation. The secret is the fact that we can replace the changing the marble positions to represent the opposite concept in the last gamewith the changing of the card orientation in the new game.

Fundamental Categorical Proposition of Aristotle

 ed the card , the its opposite NOT a is represented by the horizontally oriented card  .

If the subject is represented by a red card and predicate b represented by green card , then the fundamental categorical statement of Aristotle is represented by pairs of cards  as it is shown in the following table

The premises and conclusion of a syllogism form is one of four such statements.

Proof of the Validity of Syllogism

The game playing that simulate the proving of the validity of a syllogism includes the following steps
 

1. juxtaposing the card pairs which represent both premises of a syllogism
2. disposing the pair of same colored cards with different orientation
3. putting the card which represent the subject of the second premise as the card that represent the subject of the syllogism conclusion.

With a game like this, we can do the proving of valid syllogisms with ease, because the end result of the game is a representation of the syllogism by disposing pair(s) of opposite orientated card of the same color  in the  Leibniz’s  table below:

End notes

1. Apparently, the game is very simple using colored cards that it can be taught to kindergartners. The game can also be seen as a Sommersian arithmologic game.
2. The cards can be replaced with anything that have duplicates with the help of one sheet of paper.

Combinatoric Logic Game of Marbles

Combinatoric Logic Game of Marbles
Armahedi Mahzar (c) 2015

In my previous blog it has been shown that the combination and disposal of things can simulate the deduction of a valid syllogism. The combinatoric verification process can also be simulated by the game of arranging and disposing colored marbles and pieces of paper.

In the following it will be shown that we can simulate logical proof with the game arranging and disposing  the colorful marbles and pieces of paper. The secret is the fact that we can replace a marble represented the opposite concept with the changing of the marble’s ground.

Fundamental Categorical Proposition of Aristotle

If the subject a is represented by a red marble   and predicate b represented by green marble  , then NOT a is represented by red marble placed upon small white paper  .

Furthermore, the fundamental categorical statement of Aristotle is represented by pairs of marbles as it is shown in the following table

The premises and conclusion of a syllogism form is one of four such statements.

Proof of the Validity of Syllogism

The game playing that simulate the proving of the validity of a syllogism includes the following steps

1. juxtaposing the marble pairs which represent both premises of a syllogism
2. disposing the pair of same colored marble with different ground
3. putting the marble which represent the subject of the second premise as the marble that represent the subject of the syllogism conclusion.

With a game like this, we can do the proving of valid syllogisms with ease, because the end result of the game is a representation of the syllogism conclusion. The table below is the Leibniz table of the premises of valid syllogisms. 

End notes

1.  Apparently, the game is very simple using colored marbles  can be taught to kindergartners. The game can also be seen as a simulation of Sommersian arithmologic.
2. Unfortunately, this game can only be played with the help of additional pieces of paper.  However, with a set of colored cards without  the help of other pieces of paper, we can simulate the proving of the syllogism validity with a simpler game as I have found it. Hopefully, that will be presented in my next blog.

Solving the Tardy Bus Problem

Solving the Tardy Bus Problem
Using the Combinatoric Game of Marbles
Armahedi Mahzar (c) 2015

In previous blogs we prove the validity of classical syllogism comprising two premises involving two concepts by playing logic game of things. But classical syllogisms is just the easiest logical problems that is possible. In fact there are enormous multiplicity of problems with more than two premises involving more than three concepts. In this blog we will use the Ploucquet-Sommers game as a tool to solve a problem given by Professor Layman E.Allen    of the Yale university who created the WFF’N PROOF: a game of logic based on Polish notation.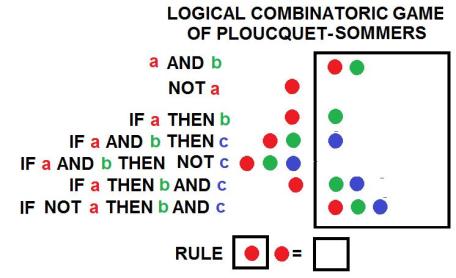

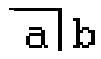The Tardy Bus Problem
One problem that can be solved with Boolean logic has many complex impicative propositions as premises. The following table shows the formation and transformation rules for such problem



Given the following three statements as premises:

1. If Bill takes the bus, then Bill misses his appointment, if the bus is late.
2. Bill shouldn’t go home, if (a) Bill misses his appointment, and (b) Bill feels downcast.
3. If Bill doesn’t get the job, then (a) Bill feels downcast, and (b) Bill should go home.

Is it valid to conclude that
Q1 –if Bill takes the bus, then Bill does get the job, if the bus is late? ___YES___NO
Q2 –Bill does get the job, if (a) Bill misses his appointment, and (b) Bill should go home? ___YES___NO
l doesn’t take the bus, or Bill doesn’t miss his appointment, if (b) Bill doesn’t get the job? ___YES___NO
Q4 –Bill doesn’t take the bus, if (a) the bus is late, and (b) Bill doesn’t get the job? ___YES___NO
Q5 –if Bill doesn’t miss his appointment, then (a) Bill shouldn’t go home, and (b) Bill doesn’t get the job? ___YES___NO
Q6 –Bill feels downcast, if (a) the bus is late, or (b) Bill misses his appointment? ___YES___NO
Q7 –if Bill does get the job, then (a) Bill doesn’t feel downcast, or (b) Bill shouldn’t go home? ___YES___NO
Q8 –if (a) Bill should go home, and Bill takes the bus, then (b) Bill doesn’t feel
downcast, if the bus is late?

Solving the problem
To answer the question we will represent the premises as combinations of colored marbles representing the concepts in the logical universe using the following rules



to get the arrangement of colored marbles for the premises is like this

By eliminating pairs of same colored marbles across the paper boundary, we got the following conclusion:

which is interpreted as Q4 having the answer YES.
So Q1, Q2. Q3, Q5, Q6, Q7 and Q8 have the answer NO.

Afternote
If you think this is a big difficult problem, my next blog will present you a gigantic problem containing 20 premises involving 18 concepts to test the power of my combinatoric game. That problem is the famous froggy problem of Lewis Carroll. Unfortunately, he died before he was able to publish the solution — but he warned that it contains “a beautiful ‘trap.’”

Combinatoric Logic Game of Things

Combinatoric Logic Game of Things

Armahedi Mahzar (c) 2015

In my sequence  of blogs I have presented variety games of things with different rules of arranging things, but single rule of disposing pair of things, all simulates the proving of valid categorical syllogisms in the table of Leibniz. In fact, all games that being discussed can simulate the proof of hypothetical and disjunctive syllogisms of the Stoic. It even can prove all tautologies of the Boolean algebra of logic.

The simplest game of logic is purely combinatoric that simulating Ploucquet method of proving syllogism which has two premises. The premises consist  of two state letters. The conclusion can be derived by disposing paired letters of similar sound but different case in the combination of premises.  The capital letters are representing universal  subject and negative predicate. The lower case letters are representing particular subject or positive predicate they represent.

Let me show you how can we play the general combinatoric game with tin soldiers used as representation of concepts or variables and a sheet of paper to differentiate the universality / negativity or particularity / positivity of the concepts by positioning the tin soldiers outside or inside the paper borders.  This convention is the reversal of the convention held in my last blog. But the new convention seems more natural.

Categorical proposition of Aristoteles

In Ploucqetian combinatoric “all a is b” is represented by Ab, “no a is b”  is represented by AB, “ some a are b” is represented by ab and “some a are not b” is represented by aB.  In the tin soldiers combinatorics game of logic They represented by the following picture

Proving Aristotlean Syllogism Validity

The simulation of the proof of the validity of Barbara syllogism by playing the tin soldiers game is shown by the following picture:

Proving Stoic Syllogism validity

The game can be used to prove the validity of the hypothetical and disjunctive syllogisms of the Stoic logicians: modus ponens, modus tollens and modus tollendo ponens.

Afternotes

The game In this blog is based on the Sommersian arithmologic. However more complex games can also be created based on Boolean and Peircean arithmologic.  As a tool such games is too complex, however  it shows that all arithmologic systems can be simulated with combinatorics games of thing.

Sommersian Chips Game of Logic

Armahedi Mahzar (c) 2015

In my previous blogs I presented a simulation of Boolean and Peircean arithmologic with games of chips. In this blog I will show you how to simulate Sommersian Arithmologic using the same chips. It will be shown that the derivation of the conclusion from two premises in the valid syllogisms is really the easiest. There are 24 valid syllogism as it is shown in the following Leibniz table:

Representing Logical Expression with Chips
Aristotle using verbal string of words to represent logical expression such as IF a THEN b. George Boole in 19th century used string of algebraic symbols to represent the mentioned logical expression as 1-a+b. In the 20th century, George Spencer-Brown used a containment of forms  to express the same logical expression as . Later, Lousis Kauffman in his Box Algebra represent the same logical expression as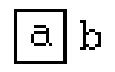.  . 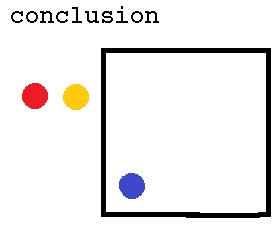Finally, I replaced Kauffman letters with colored chips  , to get Object Logic algebra the representation of the logical expression IF a THEN b is  .

Now, we can construct an arithmologic game that simulates Boolean arithmetic by representing TRUE or 1 by black chip    and variables by colored chips. Other representations for logical expressions is shown in the following table

The Categorical Proposition of Aristoteles

If a is represented by RED chip, b by a GREEN chip and 1 by a BLACK chip, the the four fundamental categoric proposition of Aristotle can be represented as it is shown in the following table.

Simulating the Syllogism Validity Proof
Reasoning by syllogism now can be simulated by three steps algorithm
1. Combined all the representation of premises with AND as the combinator.
2. Dispose all chip pairs  where the red chip is the symbol of any colored chip.
3. Read the rest as conclusion. If the rest is containing two color chips then the syllogism is valid. Otherwise it is invalid.

Proving Valid Syllogisms

To prove the Barbara syllogism, IF all m is p AND all s is m THEN all s is p, we represent s, m and p with red, green and blue chips and represent the conjunction of premises as the chips configuration above the horizontal line in the picture below.

By discarding opposite pairs of chips, we will get the chips configuration below the line which can be read as the conclusion of the syllogism.

The proof the validity of all 15 syllogisms can be derived with the help of the following table.

Beside the 15 valid syllogisms without any assumption of the existence of a certain term, there are 9 valid moods of syllogism containing existential assumption.

For example, the validity of Barbari syllogism which is containing one assumption of the existence of the subject term can be proven like this, where the the third proposition is Iss is represented by the following picture.

In the proof, we just eliminate the oppositional pair of chips above the horizontal line to get the chip configuration below the line.

The proof the validity of all 9 existential syllogisms can be shown in the following table.

Afternotes

The chips game can be used to prove hypothetical and disjunctive of the Stoic logician. In fact it can be used to prove any Boolean tautology. So it is shown that a game of concrete object can also simulate any logical proof in abstract algebraic symbols.

The objects chosen in this blog are colored chips. However the colored chips can be replaced with any objects and the black chips can be replaced with any sheets of paper. For example, the colored chips are replaced with colored marbles and the black chips are replaced with closed cards.

In this blog, logic is formulated with Sommersian algebraic symbols. The Boolean algebraic, Peircean pictorial and Sommersian literal formulations can also be simulated with similar game of concrete things. Among the three games, the Sommersian is the simplest.

All the logic games of concrete things are so easy to play that it can be taught to any kindergarten kid. Surely, we just teach them the rules of formation and transformation of the things arrangement without the logical interpretation.

Once they are skilled in the logic game playing, the algorithm will be deeply entrenched in their subconscious so it will facilitate their logical skill in later ages. Hopefully, the games can also enhanced their IQ like the WFF’n PROOF game created by professor Layman E. Allen in the Yale University.

Peircean Chips Game of Logic

Peircean Chips Game of Logic
Armahedi Mahzar © 2015

 

In my previous blog I presented a simulation of Boolean arithmologic with a game of chips. In this blog I will show you how to simulate Peircean Arithmologic using the same chips. It will be shown that the derivation of the conclusion from two premises in the valid syllogisms is very easy. There are 24 valid syllogism as it is shown in the following Leibniz table:

Representing Logical Expression with Chips

Aristotle using verbal string of words to represent logical expression such as IF a THEN b. George Boole in 19^th century used string of algebraic symbols to represent the mentioned logical expression as 1-a+b. In the 20^th century, George Spencer-Brown used a containment of forms    to express the same logical expression as . Later, Louis Kauffman in his Box Algebra represent the same logical expression as  . Finally, I replaced Kauffman letters with colored chips, to get Object Logic algebra the representation of the logical expression IF a THEN b is  .
Now, we can construct an arithmologic game that simulates Boolean arithmetic by representing TRUE or 1 by black chip and variables by colored chips. Other representations for logical expressions is shown in the following table

The Categorical Proposition of Aristoteles

If a is represented by RED chip, b by a GREEN chip and 1 by a BLACK chip, the the four fundamental categoric proposition of Aristotle can be represented as it is shown in the following table.

Simulating the Syllogism Validity Proof

Reasoning by syllogism now can be simulated by three steps algorithm

1. Combined all the representation of premises with AND as the combinator.
2. Dispose all chip pairs  where the red chip is the symbol of any colored chip.

3. Read the rest as conclusion. If the rest is containing two color chips then the syllogism is valid. Otherwise it is invalid.

Proving Valid Syllogisms

To prove the Barbara syllogism, IF all m is p AND all s is m THEN all s is p, we represent s, m and p with red, green and blue chips and represent the conjunction of premises as the chips configuration above the horizontal line in the picture below.

By discarding opposite pairs of chips, we will get the chips configuration below the line which can be read as the conclusion of the syllogism.

The proof the validity of all 15 syllogisms can be derived with the help of the following table.

Beside the 15 valid syllogisms without any assumption of the existence of a certain term, there are 9 valid moods of syllogism containing existential assumption.

For example, the validity of Barbari syllogism which is containing one assumption of the existence of the subject term can be proven like this, where the the third proposition is Iss is represented by the following picture.

In the proof, we just eliminate the oppositional pair off chips above the horizontal line to get the chip configuration below the line.

The proof the validity of all 9 existential syllogisms can be shown in the following table.

Afternotes

The chips game can be used to prove hypothetical and disjunctive of the Stoic logician. In fact it can be used to prove any Boolean tautology. So it is shown that a game of concrete objects can simulate any logical proof in abstract algebraic symbols.

The objects chosen in this blog are colored chips. However the colored chips can be replaced with any objects and the black chips can be replaced with any sheets of paper. For example, the colored chips are replaced with colored marbles and the black chips are replaced with closed cards.

In this blog, logic is formulated with Peircean algebraic symbols. However logic can also be represented Sommersian arithmetical symbols. Both Peircean pictorial and Sommersian literal formulations can also be simulated with similar game of concrete things. The new games is simpler than the Boolean game described before.

All the logic games of concrete things are so easy to play that it can be taught to any kindergarten kid. Surely, we just teach them the rules of formation and transformation of the things arrangement without the logical interpretation.

Once they skilled in the logic game playing, the algorithm will be deeply entrenched in their subconscious so it will facilitate their logical skill in later ages. Hopefully, the games can also enhanced their IQ like the Wff’n Proof game created by proessor Layman E. Allen in the Yale University.