Solving the Tardy Bus Problem

Solving the Tardy Bus Problem
Using the Combinatoric Game of Marbles
Armahedi Mahzar (c) 2015

In previous blogs we prove the validity of classical syllogism comprising two premises involving two concepts by playing logic game of things. But classical syllogisms is just the easiest logical problems that is possible. In fact there are enormous multiplicity of problems with more than two premises involving more than three concepts. In this blog we will use the Ploucquet-Sommers game as a tool to solve a problem given by Professor Layman E.Allen    of the Yale university who created the WFF’N PROOF: a game of logic based on Polish notation.

The Tardy Bus Problem
One problem that can be solved with Boolean logic has many complex impicative propositions as premises. The following table shows the formation and transformation rules for such problem



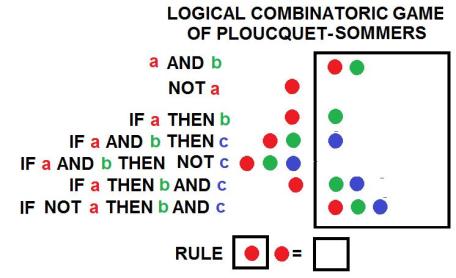
Given the following three statements as premises:

1. If Bill takes the bus, then Bill misses his appointment, if the bus is late.
2. Bill shouldn’t go home, if (a) Bill misses his appointment, and (b) Bill feels downcast.
3. If Bill doesn’t get the job, then (a) Bill feels downcast, and (b) Bill should go home.

Is it valid to conclude that
Q1 –if Bill takes the bus, then Bill does get the job, if the bus is late? ___YES___NO
Q2 –Bill does get the job, if (a) Bill misses his appointment, and (b) Bill should go home? ___YES___NO
l doesn’t take the bus, or Bill doesn’t miss his appointment, if (b) Bill doesn’t get the job? ___YES___NO
Q4 –Bill doesn’t take the bus, if (a) the bus is late, and (b) Bill doesn’t get the job? ___YES___NO
Q5 –if Bill doesn’t miss his appointment, then (a) Bill shouldn’t go home, and (b) Bill doesn’t get the job? ___YES___NO
Q6 –Bill feels downcast, if (a) the bus is late, or (b) Bill misses his appointment? ___YES___NO
Q7 –if Bill does get the job, then (a) Bill doesn’t feel downcast, or (b) Bill shouldn’t go home? ___YES___NO
Q8 –if (a) Bill should go home, and Bill takes the bus, then (b) Bill doesn’t feel
downcast, if the bus is late?

Solving the problem
To answer the question we will represent the premises as combinations of colored marbles representing the concepts in the logical universe using the following rules



to get the arrangement of colored marbles for the premises is like this

By eliminating pairs of same colored marbles across the paper boundary, we got the following conclusion:

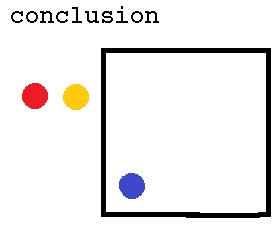
which is interpreted as Q4 having the answer YES.
So Q1, Q2. Q3, Q5, Q6, Q7 and Q8 have the answer NO.

Afternote
If you think this is a big difficult problem, my next blog will present you a gigantic problem containing 20 premises involving 18 concepts to test the power of my combinatoric game. That problem is the famous froggy problem of Lewis Carroll. Unfortunately, he died before he was able to publish the solution — but he warned that it contains “a beautiful ‘trap.’”